1. 理论基础
滨水工只求解基本的 Green-Ampt下渗模型,不涉及它的各种改进版本。其原理可参阅相关文献,如Mays (2019)等。在此仅列出其核心公式:
(2)
(3)
其中,θi为土体的初始体积含水率,θs为土体的饱和体积含水率(即土体的孔隙率),t为时间,
Fp为理论(或称潜势)累计入渗深度
(mm),fp为理论(或称潜势)入渗率
(mm/h), K为土体的渗透系数或饱和导水率
(mm/h),ψ为土体的吸力水头
(mm)。由公式 (3)可知,对于饱和土体
(Δθ
= 0)
,fp始终等于K。对于非饱和土体
(Δθ
> 0),fp随时间单调下降,其渐进极限值为K。
公式(2)和(3)代表了一个连续的下渗过程,假设地表始终有足够多的积水以保证土体中充分的下渗。实际的降雨不一定能提供足够的地表积水,这样,降雨和下渗的互动过程将产生实际累计入渗深度
F和实际入渗率f。
2. 计算方法
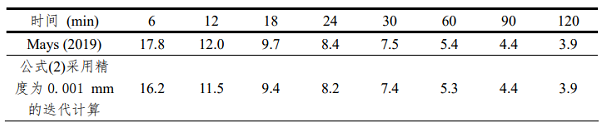
滨水工使用渐进迭代法求解公式(2)以获得 Fp, 然后按照公式(3)求得fp。公式(2)的迭代求解由假设的 Fp初值开始,迭代计算精度为0.01 mm。当前后两次Fp估计值之差的绝对值小于或等于0.01 mm时,迭代计算结束,最后的Fp估计值即为 Fp的近似解;否则,取前后两次 Fp估计值的均值,代入公式(2)继续求解。迭代采用的计算精度不同,Fp的结果当然会有所区别。如,采用迭代计算精度0.01 mm计算Mays (2019)中算例7.4.3, 滨水工所得的结果与 Mays (2019)的结果一致。当采用0.001 mm时,计算结果略有不同,如表1所示。迭代计算精度0.01 mm应该可以满足常规的工程计算要求。
当有降雨时,降雨量首先用于填充地表的坑洼。在填洼量蓄满以后,下渗开始。填洼量蓄满的时刻为td。td有可能是一个标准单元时段以内某个时刻,而不一定在一个时段的起止点。如果
td为一个时段以内某个时刻,下渗计算的第一个时间步长为
td至该时段的终点。之后,下渗计算的时间步长恢复至标准时间步长(即用户给定的计算时间步长)。
如果在一个时间段内有下渗发生,在这个时间段结束时,
fp会被修正,记为fpu;具体方法在后面说明。fpu称为修正后的潜势入渗率,代表了一个实时的入渗潜力,是土体与实际降雨过程互动的结果。如果在一个时间段内没有下渗发生,这个时间段结束时的fpu则等于前一时间段结束时的fpu。
累计入渗深度的起始值为零;即,当下渗开始时,
F =
Fp
= 0。对于非饱和土体
(∆θ >
0)
,由公式(3)可知,在理论上,
fp的起始值为正无穷大,即
fp
= +∞。在这种情况下,
滨水工假设fp和fpu的起始值均为正无穷大(无具体数值),并进而假设实际入渗率(
f)的起始值等于下渗开始时刻的降雨强度。
由前所述,公式(2)用于计算潜势入渗深度
Fp。如果实际雨量低于土体的下渗能力,公式(2)所代表的连续充分下渗过程会被扰乱,故公式(2)计算中的时间项不能采用下渗开始以来的自然累计时间。此时,公式(2)需要一个用于潜势入渗计算的等效时间,te。这个等效时间虚拟了一个自下渗开始以来公式(2)所经历的累计时间。由公式(2),
其中,
te(t)为t时刻的潜势入渗等效时间。在t之前,如果降雨量始终能够保证土体中充分的下渗,
te=
t;否则,te<
t
。
如图1所示,在任一时刻t1,fpu和i之间可能存在三种情况。时刻
t1后的计算时间步长为dt,下一时刻为t2。在情况(1)或(2)中,
i(t1)
< fpu(t1)
;在情况(3)中,i(t1)≥
fpu
(t1)。这三种情况亦可参阅
Alan A. Smith
Inc.
(2004)。如,对于非饱和土体,下渗的初始时刻属于情况(1)或(2)。下渗计算在这三种情况中将有所区别。
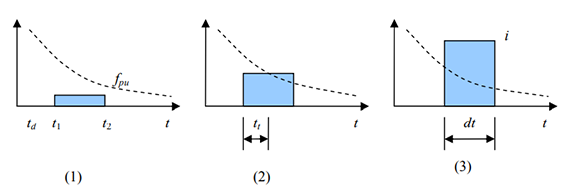
图1:在任一时刻fpu和i之间的三种情况
- 情况(1):在t1和t2之间,所有降雨会下渗,没有净雨产生。
- 情况(2):dt被分为两段,前一段长度为tt,后一段长度为dt-tt 。在前一段,所有降雨会下渗,没有净雨产生。在后一段,部分降雨将成为净雨。
- 情况(3):在t1和t2之间,入渗按该时段内的fpu发生,部分降雨将成为净雨。
情况(1)或(2)可由积水时间(tp)来进一步判别。由Alan A. Smith Inc. (2004) 所示,在t1之后,对任意降雨强度i (mm/h),可结合公式(3)获得一个对应的tp:
在情况(1)中,tp ≥ dt。在情况(2)中,tp < dt,此时tt = tp。
2.1 情况(1):i( t1) < fpu(t1), tp ≥ dt
主要计算内容如下:
- f(t1) = i(t1)
- t1和t2之间的下渗量F[t1,t2] = i(t1)⋅dt。与F(t1)累加,可以获得td和 t2之间的总下渗量F(t2)。
- 由公式(3)获得fpu(t2)
- 由公式(4)获得te(t2)
- 这个时段的净雨(ie)为零
2.2 情况(2):i(t1) < fpu(t1), tp < dt
主要计算内容如下:
- f(t1) = i(t1)
- tt = tp
- t1和t1+tt之间的下渗量F[t1,t1+tt] =i(t1)⋅tt。与F(t1)累加,可以获得t1+tt处的总下渗量 F(t1+tt)。
- F(t2)可结合F(t1+tt)根据公式(2)的迭代计算求得,但需要te(t2)。首先由公式(4)获得 te(t1+tt),然后,
- 基于te(t2),由公式(2)获得F(t2)。
- 由公式(3)获得fpu(t2)
- t1处的净雨,ie(t1),可按下式求得:
- 注意:在一个时间步长内,ie是该步长内的平均值。
2.3 情况(3): i(t1) ≥ fpu (t1)
主要计算内容如下:
- f(t1) = fpu (t1)
- te(t2)由te(t1)直接累加:
- 基于te(t2),由公式(2)获得F(t2)。
- 由公式(3)获得fpu(t2)
- 由公式(7)获得ie(t1)
3. 参数输入
用户需要在参数输入页面上给定以下信息:
- θi, θs, K和ψ
- 时间步长 (min)
- 这是指计算所采用的时间步长。在需要生成净雨过程时,这个时间步长必须和降雨强度过程的时间步长一致。
- 总时间步长数
- 这是指分析时段内的总时间步长数,即进行计算的总时长。当需要生成净雨过程时,如果用户给定的分析时段短于或等于降雨强度过程,滨水工的计算及结果展示将采用降雨强度过程的时长;如果用户给定的分析时段长于降雨强度过程,计算及结果展示将采用用户给定的分析时长,但假定降雨结束之后的降雨强度均为零。这一项只能输入整数,不得带有小数点。
- 地表初期填洼量 (mm)
- 这一项仅在需要生成净雨过程时输入。地表初期填洼量可以为零,即不考虑这一项,此时应输入0。
- 降雨强度过程 (mm/h)
- 这一项仅在需要生成净雨过程时输入。降雨强度过程的格式为数值和逗号。由数值起始,一个数值后面紧跟一个逗号,但最后一个数值后不能有逗号。滨水工仅接受半角的逗号,不接受全角的逗号。一个降雨强度值为一个时间步长内的恒定值。降雨强度过程的时间步长必须和分析计算采用的时间步长一致。如降雨强度过程的总降雨量不足以填满初期填洼量,程序会自动终止,不会进行下渗计算。
对于需要页面输入的参数,请务必输入数值。否则滨水工无法有效运行。
4. 结果输出
滨水工采用Python 3.9.0 (van
Rossum等
2022)开发本计算程序。
在输出的计算结果图上,为方便与降雨强度比较,f用柱状图表示;即,一个时间步长起点处的f显示在整个步长内。
地表坑洼的充填速率即单位时间内的填洼量(或消耗的降雨量),按降雨初期相应时段内的降雨强度表示。
如果无需生成净雨过程,滨水工仅输出fp。如果降雨量不足以蓄满地表的坑洼,没有下渗产生,也不会有净雨产生,此时滨水工仅输出fp。
在输出的数值结果中,净雨强度按一个步长内的平均值给出,见公式 (7)。然而,出于展示目的,对于图1中的情况(2),结果图中按三角形近似绘出净雨强度。
参考文献
Alan A. Smith Inc. (2004) MIDUSS Version 2 Reference Manual
Mays, L.W. (2019) Water Resources Engineering, 3rd Edition, Wiley.
van Rossum, G., and the Python Development Team (2022)
The
Python Language Reference (Release 3.9.13), Python
Software Foundation (http://www.python.org)